티스토리 뷰
Problem
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.
Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: trueExample 2:
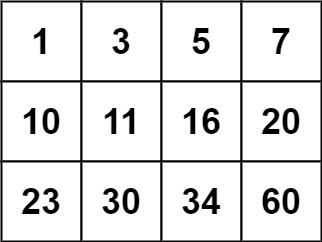
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: falseConstraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -10^4 <= matrix[i][j], target <= 10^4
Solution
정수 행렬이 주어지는데 각 열과 행은 오름차순으로 정렬되어있습니다.
타겟 정수가 행렬에 존재하는지 여부를 반환하는 문제입니다.
각 행을 탐색하면서 이진탐색으로 타겟 정수를 찾으면 됩니다.
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
for (int[] row : matrix) {
if (target <= row[n - 1]) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (target == row[mid]) {
return true;
}
if (target < row[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
}
}
return false;
}
}
Test
package io.lcalmsky.leetcode.search_a_2d_matrix;
import static org.junit.jupiter.api.Assertions.assertAll;
import static org.junit.jupiter.api.Assertions.assertEquals;
import org.junit.jupiter.api.Test;
class SolutionTest {
@Test
void givenMatrix_whenSearchesTarget_thenReturnsWhetherExists() {
assertAll(
() -> test(new int[][]{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 50}}, 3, true),
() -> test(new int[][]{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 50}}, 13, false)
);
}
private void test(int[][] givenArray, int givenTarget, boolean expected) {
// when
Solution searchA2dMatrix = new Solution();
boolean actual = searchA2dMatrix.searchMatrix(givenArray, givenTarget);
// then
assertEquals(expected, actual);
}
}'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode] 146. LRU Cache (0) | 2023.07.03 |
|---|---|
| [LeetCode] 78. Subsets (0) | 2023.07.02 |
| [LeetCode] 46. Permutations (0) | 2023.06.30 |
| [LeetCode] 230. Kth Smallest Element in a BST (0) | 2023.06.29 |
| [LeetCode] 334. Increasing Triplet Subsequence (0) | 2023.06.28 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 스프링 데이터 jpa
- 클린 아키텍처
- intellij
- Linux
- leetcode
- 스프링부트
- spring boot app
- Spring Boot JPA
- proto3
- spring boot jwt
- Java
- 함께 자라기
- Spring Boot
- JSON
- @ManyToOne
- JPA
- 알고리즘
- 스프링 부트
- Spring Data JPA
- spring boot application
- r
- Jackson
- Spring Boot Tutorial
- 스프링 부트 애플리케이션
- QueryDSL
- 함께 자라기 후기
- 스프링 부트 튜토리얼
- 스프링 부트 회원 가입
- 헥사고날 아키텍처
- gRPC
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
글 보관함
