티스토리 뷰
Problem
According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."
The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
- Any live cell with fewer than two live neighbors dies as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.
Example 1:
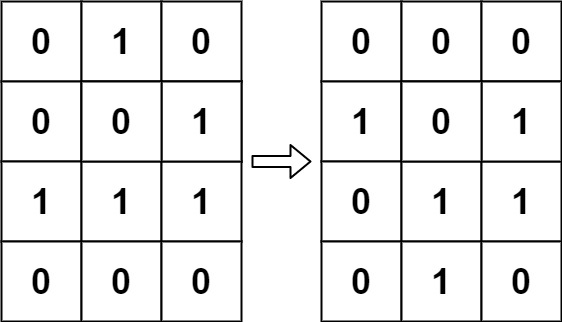
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]Example 2:
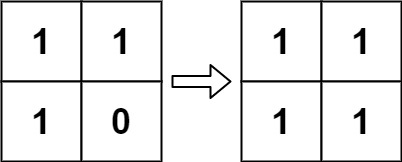
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]Constraints:
- m == board.length
- n == board[i].length
- 1 <= m, n <= 25
- board[i][j] is 0 or 1.
Follow up:
- Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
- In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?
Solution
m * n개의 그리드로 구성된 보드가 주어지고 각 셀의 초기 상태는 life(1) 또는 dead(0)를 가집니다.
각 셀은 네 가지 규칙을 사용하여 수평, 수직, 대각선으로 구성된 이웃 셀과 상호 작용 합니다.
- 살아있는 인접 셀이 2개 미만인 셀은 죽습니다.
- 살아있는 인접 셀이 2~3개인 셀은 다음 세대까지 살아갑니다.
- 살아있는 인접 셀이 3개 초과인 셀은 인구 과잉으로 죽습니다.
- 세 개의 죽은 셀은 살아있는 셀이 됩니다.
주어진 보드의 다음 상태를 반환하는 문제입니다.
public class Solution {
private final static int LIVE = 2;
private final static int DEAD = 3;
private final static int[][] DIRECTIONS = {{1, 0}, {-1, 0}, {0, 1}, {0, -1},
{1, -1}, {1, 1}, {-1, -1}, {-1, 1}};
public void gameOfLife(int[][] board) {
if (board == null || board.length == 0 || board[0].length == 0) {
return;
}
int m = board.length;
int n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int count = 0;
for (int[] dir : DIRECTIONS) { // (1)
int row = i + dir[0];
int col = j + dir[1];
if (row < 0 || col < 0 || row >= m || col >= n) {
continue;
}
if (board[row][col] == 1 || board[row][col] == DEAD) { // (2)
count++;
}
}
if (board[i][j] == 1 && (count < 2 || count > 3)) { // (3)
board[i][j] = DEAD;
} else if (board[i][j] == 0 && count == 3) { // (4)
board[i][j] = LIVE;
}
}
}
for (int i = 0; i < m; i++) { // (5)
for (int j = 0; j < n; j++) {
if (board[i][j] == LIVE) {
board[i][j] = 1;
} else if (board[i][j] == DEAD) {
board[i][j] = 0;
}
}
}
}
}- 각 셀의 8 방향을 조사합니다.
- 현재 셀 주변의 죽은 셀 개수를 셉니다.
- 현재 셀이 죽은 셀이고, 주변의 죽은 셀 개수가 2개 미만 또는 3개 초과일 때 미래에 죽을 상태로 변경합니다. 여기서 똑같이 1을 사용하지 않는 이유는 다음 결과에 영향을 주기 때문입니다.
- 현재 셀이 살아있고, 주변에 죽은 셀이 3개인 경우 미래에 살아있는 상태로 변경합니다.
- 미래 상태를 업데이트 시킵니다.
Test
package io.lcalmsky.leetcode.game_of_life;
import static org.junit.jupiter.api.Assertions.assertAll;
import static org.junit.jupiter.api.Assertions.assertArrayEquals;
import org.junit.jupiter.api.Test;
class SolutionTest {
@Test
void testAll() {
assertAll(
() -> test(new int[][]{{0, 1, 0}, {0, 0, 1}, {1, 1, 1}, {0, 0, 0}},
new int[][]{{0, 0, 0}, {1, 0, 1}, {0, 1, 1}, {0, 1, 0}}),
() -> test(new int[][]{{1, 1}, {1, 0}}, new int[][]{{1, 1}, {1, 1}})
);
}
private void test(int[][] given, int[][] expected) {
// when
Solution solution = new Solution();
solution.gameOfLife(given);
// then
assertArrayEquals(expected, given);
}
}'Algorithm > LeetCode' 카테고리의 다른 글
| 700. Search in a Binary Search Tree (0) | 2022.04.27 |
|---|---|
| 991. Broken Calculator (0) | 2022.04.26 |
| 856. Score of Parentheses (0) | 2022.04.24 |
| 31. Next Permutation (0) | 2022.04.23 |
| 344. Reverse String (0) | 2022.04.22 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- Java
- proto3
- Spring Boot JPA
- 알고리즘
- JPA
- 헥사고날 아키텍처
- Spring Data JPA
- r
- 스프링 부트 튜토리얼
- 함께 자라기 후기
- JSON
- QueryDSL
- 스프링부트
- 클린 아키텍처
- leetcode
- intellij
- 스프링 부트 애플리케이션
- spring boot app
- gRPC
- 함께 자라기
- Spring Boot Tutorial
- spring boot application
- 스프링 데이터 jpa
- 스프링 부트 회원 가입
- Linux
- 스프링 부트
- @ManyToOne
- spring boot jwt
- Jackson
- Spring Boot
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
