티스토리 뷰
Problem
You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.
Return the order of the largest axis-aligned plus sign of 1's contained in grid. If there is none, return 0.
An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.
Example 1:
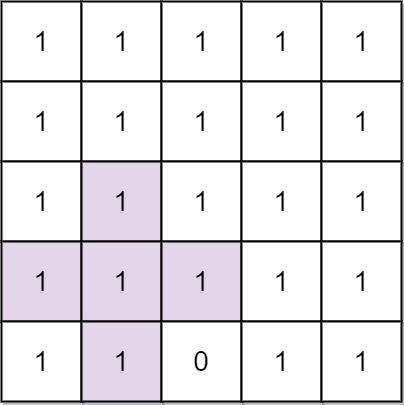
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.Example 2:

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.Constraints:
- 1 <= n <= 500
- 1 <= mines.length <= 5000
- 0 <= xi, yi < n
- All the pairs (xi, yi) are unique.
Solution
n * n 이진 그리드와 지뢰의 좌표들이 주어질 때 지뢰를 밟지 않으면서 그릴 수 있는 최대 크기의 십자가의 변의 길이를 반환하는 문제입니다.
brute force로 하나씩 다 살펴보면 시간복잡도가 너무 높아지기 때문에 DP(Dynamic Programming)를 이용해 시간 복잡도를 낮출 수 있습니다.
import java.util.HashSet;
import java.util.Set;
public class Solution {
public int orderOfLargestPlusSign(int n, int[][] mines) {
Set<Integer> banned = new HashSet<>(); // (1)
for (int[] mine : mines) { // (1)
banned.add(mine[0] * n + mine[1]);
}
int[][] dp = new int[n][n];
int count;
for (int row = 0; row < n; row++) { // (2)
count = 0;
for (int col = 0; col < n; col++) {
count = banned.contains(row * n + col) ? 0 : count + 1;
dp[row][col] = count;
}
count = 0;
for (int col = n - 1; col >= 0; col--) {
count = banned.contains(row * n + col) ? 0 : count + 1;
dp[row][col] = Math.min(dp[row][col], count);
}
}
int result = 0;
for (int col = 0; col < n; col++) { // (3)
count = 0;
for (int row = 0; row < n; row++) {
count = banned.contains(row * n + col) ? 0 : count + 1;
dp[row][col] = Math.min(dp[row][col], count);
}
count = 0;
for (int row = n - 1; row >= 0; row--) {
count = banned.contains(row * n + col) ? 0 : count + 1;
dp[row][col] = Math.min(dp[row][col], count);
result = Math.max(result, dp[row][col]);
}
}
return result;
}
}(1) 공간 복잡도를 아끼기 위해 지뢰의 좌표를 저장하는 게 아니라 수식을 통해 고유한 숫자로 저장합니다. n * row + col로 저장하면 n * n 행렬에 대해 고유한 값을 가집니다.
(2) 각 행을 기준으로 열을 탐색하는데 왼쪽에서 오른쪽으로 한 번, 오른쪽에서 왼쪽으로 한 번 탐색하면서 지뢰가 있으면 0을, 그렇지 않으면 1씩 증가시키며 값을 대입합니다. 역방향으로 진행할 때는 기존 count값과 비교하여 최솟값을 대입합니다.
(3) 각 열을 기준으로 행을 탐색하는데 마찬가지로 위에서 아래로 한 번, 아래서 위로 한 번 탐색하면서 같은 방식으로 값을 대입하는데 이미 값이 존재하므로 기존 count값과 비교하여 최솟값을 대입합니다.
1번 예시가 위 알고리즘에 의해 어떻게 동작하는지 살펴보면,
- (2)번 수행
[1, 2, 3, 4, 5] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [1, 2, 3, 4, 5] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[0, 0, 0, 0, 0] -> [0, 0, 0, 0, 0] -> [0, 0, 0, 0, 0] -> [0, 0, 0, 0, 0] -> [1, 2, 3, 4, 5]
[0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0]
[0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0]
[1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1]
[0, 0, 0, 0, 0] [1, 2, 3, 4, 5] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [0, 0, 0, 0, 0] [1, 2, 0, 1, 2] [1, 1, 0, 1, 1] - (3)번 수행
[1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 1, 3, 2, 1] [1, 1, 3, 2, 1] [1, 1, 1, 2, 1]
[1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 2, 2, 1]
[1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1] -> [1, 2, 3, 2, 1]
[1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1] [1, 2, 3, 2, 1]
[1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1]
[1, 1, 1, 2, 1] [1, 1, 1, 1, 1] [1, 1, 1, 1, 1] [1, 1, 1, 1, 1] [1, 1, 1, 1, 1]
[1, 2, 2, 2, 1] [1, 2, 2, 2, 1] [1, 2, 2, 2, 1] [1, 2, 2, 2, 1] [1, 2, 2, 2, 1]
[1, 2, 2, 2, 1] -> [1, 2, 2, 2, 1] -> [1, 2, 2, 2, 1] -> [1, 2, 2, 2, 1] -> [1, 2, 2, 2, 1]
[1, 2, 1, 2, 1] [1, 2, 1, 2, 1] [1, 2, 1, 2, 1] [1, 2, 1, 2, 1] [1, 2, 1, 2, 1]
[1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1] [1, 1, 0, 1, 1]위와 같은 절차를 통해 최종적으로 가장 긴 값인 2가 반환됩니다.
여기서 가장 중요한 건 (2), (3)번에서 역방향으로도 탐색하면서 count 값을 다시 계산해주는 것인데 이렇게 하지 않으면 지뢰 기준으로 최솟값에 대한 계산이 이뤄지지 않기 때문입니다.
Test
package io.lcalmsky.leetcode.largest_plus_sign;
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.assertAll;
import static org.junit.jupiter.api.Assertions.assertEquals;
class SolutionTest {
@Test
void givenNbyNBinaryGridAndMines_whenFindLargestPlusSign_thenCorrect() {
assertAll(
() -> test(5, new int[][]{{4, 2}}, 2),
() -> test(5, new int[][]{{4, 1}}, 3),
() -> test(1, new int[][]{{0, 0}}, 0)
);
}
private void test(int n, int[][] mines, int expected) {
// when
Solution solution = new Solution();
int actual = solution.orderOfLargestPlusSign(n, mines);
// then
assertEquals(expected, actual);
}
}'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode - Daily Challenge] 917. Reverse Only Letters (0) | 2021.09.15 |
|---|---|
| [LeetCode - Daily Challenge] 1189. Maximum Number of Balloons (0) | 2021.09.14 |
| [LeetCode - Daily Challenge] 848. Shifting Letters (0) | 2021.09.09 |
| [LeetCode - Daily Challenge] 206. Reverse Linked List (0) | 2021.09.08 |
| [LeetCode - Daily Challange] 1629. Slowest Key (0) | 2021.09.07 |
- Total
- Today
- Yesterday
- proto3
- leetcode
- r
- QueryDSL
- 스프링 데이터 jpa
- 알고리즘
- 헥사고날 아키텍처
- JPA
- spring boot jwt
- 스프링 부트 애플리케이션
- spring boot application
- 스프링 부트
- 스프링부트
- Spring Boot Tutorial
- JSON
- gRPC
- Jackson
- 함께 자라기
- 함께 자라기 후기
- Spring Data JPA
- @ManyToOne
- Java
- 클린 아키텍처
- Linux
- Spring Boot
- 스프링 부트 회원 가입
- intellij
- spring boot app
- 스프링 부트 튜토리얼
- Spring Boot JPA
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
